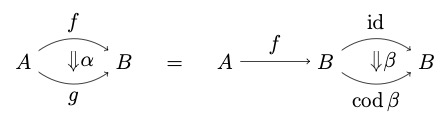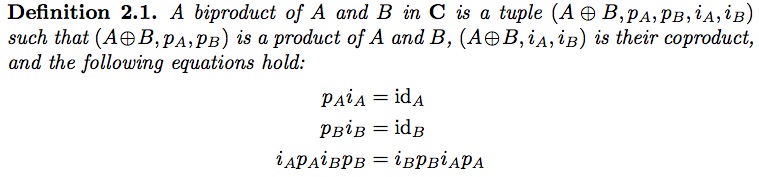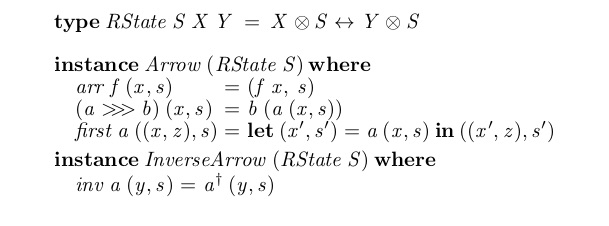
Inner automorphisms as 2-cells.
Hofstra, P., & Karvonen, M. (2024). Inner automorphisms as 2-cells. Theory and Applications of Categories, Vol. 42, No. 2, 19-40.
PDF
BibTeX
ArXiv
Journal
Abstract
Nutshell
Abstract inner automorphisms can be used to promote any category into a 2-category, and we study two-dimensional limits and colimits in the resulting 2-categories. Existing connected colimits and limits in the starting category become two-dimensional colimits and limits under fairly general conditions. Under the same conditions, colimits in the underlying category can be used to build many notable two-dimensional colimits such as coequifiers and coinserters. In contrast, disconnected colimits or genuinely 2-categorical limits such as inserters and equifiers and cotensors cannot exist unless no nontrivial abstract inner automorphisms exist and the resulting 2-category is locally discrete. We also study briefly when an ordinary functor can be extended to a 2-functor between the resulting 2-categories.
Given a strict 2-category, if its 2-cells come from something like inner automorphisms, then its 2-dimensional (co)limit behavior can be understood by studying 1-dimensional (co)limit behavior and the inner automorphism groups. For example, HNN-extensions of groups can be understood as certain coinserters in the
2-category of groups: this 2-category has coinserters (≈HNN-extensions) essentially because the 1-category of groups is finitely cocomplete, and the forgetful functor to sets is representable.
Inner autoequivalences in general and those of monoidal categories in particular
Hofstra, P., & Karvonen, M. (2024). Inner autoequivalences in general and those of monoidal categories in particular. Journal of Pure and Applied Algebra, Volume 228, Issue 11, 107717.
PDF
BibTeX
ArXiv
Journal
Abstract
Nutshell
We develop a general theory of (extended) inner autoequivalences of objects of any 2-category, generalizing the theory of isotropy groups to the 2-categorical setting. We show how dense subcategories let one compute isotropy in the presence of binary coproducts, unifying various known one-dimensional results and providing tractable computational tools in the two-dimensional setting. In particular, we show that the isotropy 2-group of a monoidal category coincides with its Picard 2-group, i.e., the 2-group on its weakly invertible objects.
Our main result states that inner autoequivalences of monoidal categories are essentially the same as conjugations by a weakly invertible element. For this to be a theorem, there needs to be a general theory of inner autoequivalences, and indeed there is: developing that is the other main contribution.
Categorical composable cryptography: extended version
Broadbent, A., & Karvonen, M. (2023). Categorical composable cryptography: extended version. Logical Methods in Computer Science, volume 19, issue 4, 30:1-30:46.
PDF
BibTeX
ArXiv
Journal
Abstract
Nutshell
We formalize the simulation paradigm of cryptography in terms of category theory and show that protocols secure against abstract attacks form a symmetric monoidal category, thus giving an abstract model of composable security definitions in cryptography. Our model is able to incorporate computational security, set-up assumptions and various attack models such as colluding or independently acting subsets of adversaries in a modular, flexible fashion. We conclude by using string diagrams to rederive the security of the one-time pad, correctness of Diffie-Hellman key exchange and no-go results concerning the limits of bipartite and tripartite cryptography, ruling out e.g., composable commitments and broadcasting. On the way, we exhibit two categorical constructions of resource theories that might be of independent interest: one capturing resources shared among multiple parties and one capturing resource conversions that succeed asymptotically.
Roughly speaking, a categorical version of abstract/constructive cryptography. Extended version of the FoSSaCS paper below.
Closing Bell: Boxing Black Box Simulations in the Resource Theory of Contextuality
Barbosa, R. S., Karvonen, M., & Mansfield, S. (2023). Closing Bell: Boxing Black Box Simulations in the Resource Theory of Contextuality. In Samson Abramsky on Logic and Structure in Computer Science and Beyond.
PDF
BibTeX
ArXiv
Book Chapter
Abstract
Nutshell
This chapter contains an exposition of the sheaf-theoretic framework for contextuality emphasising resource-theoretic aspects, as well as some original results on this topic. In particular, we consider functions that transform empirical models on a scenario S to empirical models on another scenario T, and characterise those that are induced by classical procedures between S and T corresponding to 'free' operations in the (non-adaptive) resource theory of contextuality. We construct a new 'hom' scenario built from S and T, whose empirical models induce such functions. Our characterisation then boils down to being induced by a non-contextual model. We also show that this construction on scenarios provides a closed structure on the category of measurement scenarios.
An exposition of the sheaf-theoretic framework for contextuality emphasising resource-theoretic aspects, as well as some original results on this topic.
Categorical composable cryptography
Broadbent, A., & Karvonen, M. (2022). Categorical composable cryptography. In Foundations of Software Science and Computation Structures (FoSSaCS) 2022.
PDF
BibTeX
ArXiv
Proceedings
Abstract
Nutshell
We formalize the simulation paradigm of cryptography in terms of category theory and show that protocols secure against abstract attacks form a symmetric monoidal category, thus giving an abstract model of composable security definitions in cryptography. Our model is able to incorporate computational security, set-up assumptions and various attack models such as colluding or independently acting subsets of adversaries in a modular, flexible fashion. We conclude by using string diagrams to rederive the security of the one-time pad and no-go results concerning the limits of bipartite and tripartite cryptography, ruling out e.g., composable commitments and broadcasting.
Roughly speaking, a categorical version of abstract/constructive cryptography. See the extended version above.

Neither Contextuality nor Nonlocality Admits Catalysts
Karvonen, M. (2021). Neither Contextuality nor Nonlocality Admits Catalysts. Phys. Rev. Lett. 127, 160402
PDF
BibTeX
ArXiv
Journal
Abstract
Nutshell
We show that the resource theory of contextuality does not admit catalysts, i.e., there are no correlations that can enable an otherwise impossible resource conversion and still be recovered afterward. As a corollary, we observe that the same holds for nonlocality. As entanglement allows for catalysts, this adds a further example to the list of "anomalies of entanglement," showing that nonlocality and entanglement behave differently as resources. We also show that catalysis remains impossible even if, instead of classical randomness, we allow some more powerful behaviors to be used freely in the free transformations of the resource theory.
It turns out that there are no catalysts for contextuality nor for non-locality. This is in contrast with entanglement, for which catalysts famously exist.
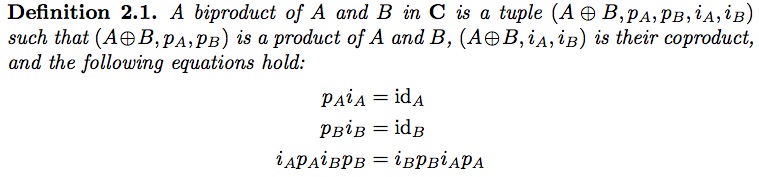
Biproducts without pointedness
Karvonen, M. (2020). Biproducts without pointedness. Cahiers de topologie et géométrie différentielle catégoriques, Vol LXI, Issue 3, 229-238.
PDF
BibTeX
ArXiv
Journal
Abstract
Nutshell
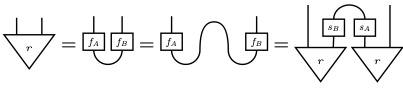
We show how to define biproducts up to isomorphism in an arbitrary category without assuming any enrichment. The resulting notion coincides with the usual definitions whenever all binary biproducts exist or the category is suitably enriched, resulting in a modest yet strict generalization otherwise. We also characterize when a category has all binary biproducts in terms of an ambidextrous adjunction. Finally, we give some new examples of biproducts that our definition recognizes.
Turns out one can define a well-behaved notion of a biproduct in any category without assuming pointedness.

A comonadic view of simulation and quantum resources
Abramsky, S., Barbosa, R. S., Karvonen, M., & Mansfield, S. (2019). A comonadic view of simulation and quantum resources. In Logic in Computer Science (LICS) 2019.
PDF
BibTeX
ArXiv
Proceedings
Abstract
Nutshell
We study simulation and quantum resources in the setting of the sheaf-theoretic approach to contextuality and non-locality. Resources are viewed behaviourally, as empirical models. In earlier work, a notion of morphism for these empirical models was proposed and studied. We generalize and simplify the earlier approach, by starting with a very simple notion of morphism, and then extending it to a more useful one by passing to a co-Kleisli category with respect to a comonad of measurement protocols. We show that these morphisms capture notions of simulation between empirical models obtained via `free' operations in a resource theory of contextuality, including the type of classical control used in measurement-based quantum computation schemes.
We improve on the ideas in the QPL paper below.
Limits in dagger categories
Heunen, C., & Karvonen, M. (2019). Limits in dagger categories. Theory and Applications of Categories, Vol. 34, No. 18, 468-513.
PDF
BibTeX
ArXiv
Journal
Abstract
Nutshell
We develop a notion of limit for dagger categories, that we show is suitable in the following ways: it subsumes special cases known from the literature; dagger limits are unique up to unitary isomorphism; a wide class of dagger limits can be built from a small selection of them; dagger limits of a fixed shape can be phrased as dagger adjoints to a diagonal functor; dagger limits can be built from ordinary limits in the presence of polar decomposition; dagger limits commute with dagger colimits in many cases.
We define a notion of limit suitable for dagger categories and explore it.
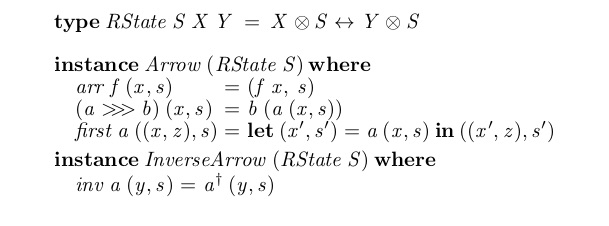
Reversible effects as inverse arrows
Heunen, C., Kaarsgaard, R., & Karvonen, M. (2018). Reversible effects as inverse arrows. Proceedings of MFPS 2018. ENTCS, 341, 179-199.
PDF
BibTeX
ArXiv
Proceedings
Abstract
Nutshell
Reversible computing models settings in which all processes can be reversed. Applications include low-power computing, quantum computing, and robotics. It is unclear how to represent side-effects in this setting, because conventional methods need not respect reversibility. We model reversible effects by adapting Hughes' arrows to dagger arrows and inverse arrows. This captures several fundamental reversible effects, including serialization and mutable store computations. Whereas arrows are monoids in the category of profunctors, dagger arrows are involutive monoids in the category of profunctors, and inverse arrows satisfy certain additional properties. These semantics inform the design of functional reversible programs supporting side-effects.
We study (reversible) side-effects in a reversible programming language. As reversible computing can be modelled by inverse categories, we model side-effects using a notion of arrow suitable for inverse categories. Since inverse categories can be defined as certain dagger categories, we also develop a notion of a dagger arrow.

Categories of Empirical Models
Karvonen, M. (2018). Categories of empirical models. Proceedings of QPL 2018, EPTCS 287, pp. 239-252.
PDF
BibTeX
ArXiv
Abstract
Nutshell
A notion of morphism that is suitable for the sheaf-theoretic approach to contextuality is developed, resulting in a resource theory for contextuality. The key features involve using an underlying relation rather than a function between measurement scenarios, and allowing for stochastic mappings of outcomes to outcomes. This formalizes an intuitive idea of using one empirical model to simulate another one with the help of pre-shared classical randomness. This allows one to reinterpret concepts and earlier results in terms of morphisms. Most notably: non-contextual models are precisely those allowing a morphism from the terminal object; contextual fraction is functorial; Graham-reductions induce morphisms, reinterpreting Vorob'evs theorem; contextual models cannot be cloned.
Formalizes an intuitive idea of using one empirical model to simulate another one with the help of pre-shared classical randomness, resulting in a resource theory for contextuality. Arguably the theory is superseded by the framework of the LICS paper above.
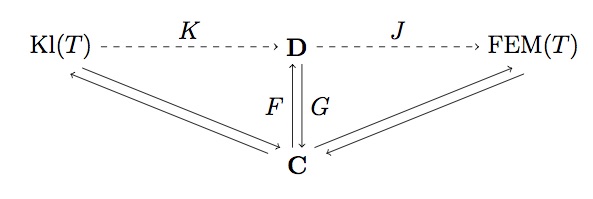
Monads on dagger categories
Heunen, C., & Karvonen, M. (2016). Monads on dagger categories. Theory and Applications of Categories, Vol. 31, No. 35, 1016-1043.
PDF
BibTeX
ArXiv
Journal
Abstract
Nutshell
The theory of monads on categories equipped with a dagger (a contravariant identity-on-objects involutive endofunctor) works best when everything respects the dagger: the monad and adjunctions should preserve the dagger, and the monad and its algebras should satisfy the so-called Frobenius law. Then any monad resolves as an adjunction, with extremal solutions given by the categories of Kleisli and Frobenius-Eilenberg-Moore algebras, which again have a dagger. We characterize the Frobenius law as a coherence property between dagger and closure, and characterize strong such monads as being induced by Frobenius monoids.
This is the extended version of the previous conference paper. When everything respects the dagger, one gets a nice theory of dagger monads analogous to the usual one.

Reversible monadic computing
Heunen, C., & Karvonen, M. (2015). Reversible monadic computing. Electronic Notes in Theoretical Computer Science, 319, 217-237.
PDF
BibTeX
ArXiv
Proceedings
Abstract
Nutshell
We extend categorical semantics of monadic programming to reversible computing, by considering monoidal closed dagger categories: the dagger gives reversibility, whereas closure gives higher-order expressivity. We demonstrate that Frobenius monads model the appropriate notion of coherence between the dagger and closure by reinforcing Cayley's theorem; by proving that effectful computations (Kleisli morphisms) are reversible precisely when the monad is Frobenius; by characterizing the largest reversible subcategory of Eilenberg-Moore algebras; and by identifying the latter algebras as measurements in our leading example of quantum computing. Strong Frobenius monads are characterized internally by Frobenius monoids.
First steps towards a theory of dagger monads. Arguably superseded by the TAC paper above.